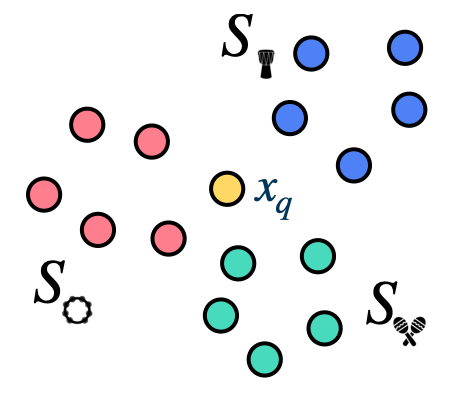Building a Prototypical Network
Contents
Building a Prototypical Network#
In this part of the tutorial, we’ll be building the prediction routine for a prototypical network in PyTorch.
To recap, prototypical networks are a type of metric-based few-shot learning method. They require a backbone model, which is used to compute the embeddings of the examples in the support and query sets. The prototypical network then creates a single prototype for each class in the support set, which is the mean of the embeddings of all the examples in the support set for that class. To classify a query example, the model compares it to each prototype using the squared Euclidean distance and applies a softmax function to the negated distances to obtain a probability distribution over the classes. The query example is then assigned to the class with the highest probability. This enables the model to learn to classify new classes using only a few examples per class.
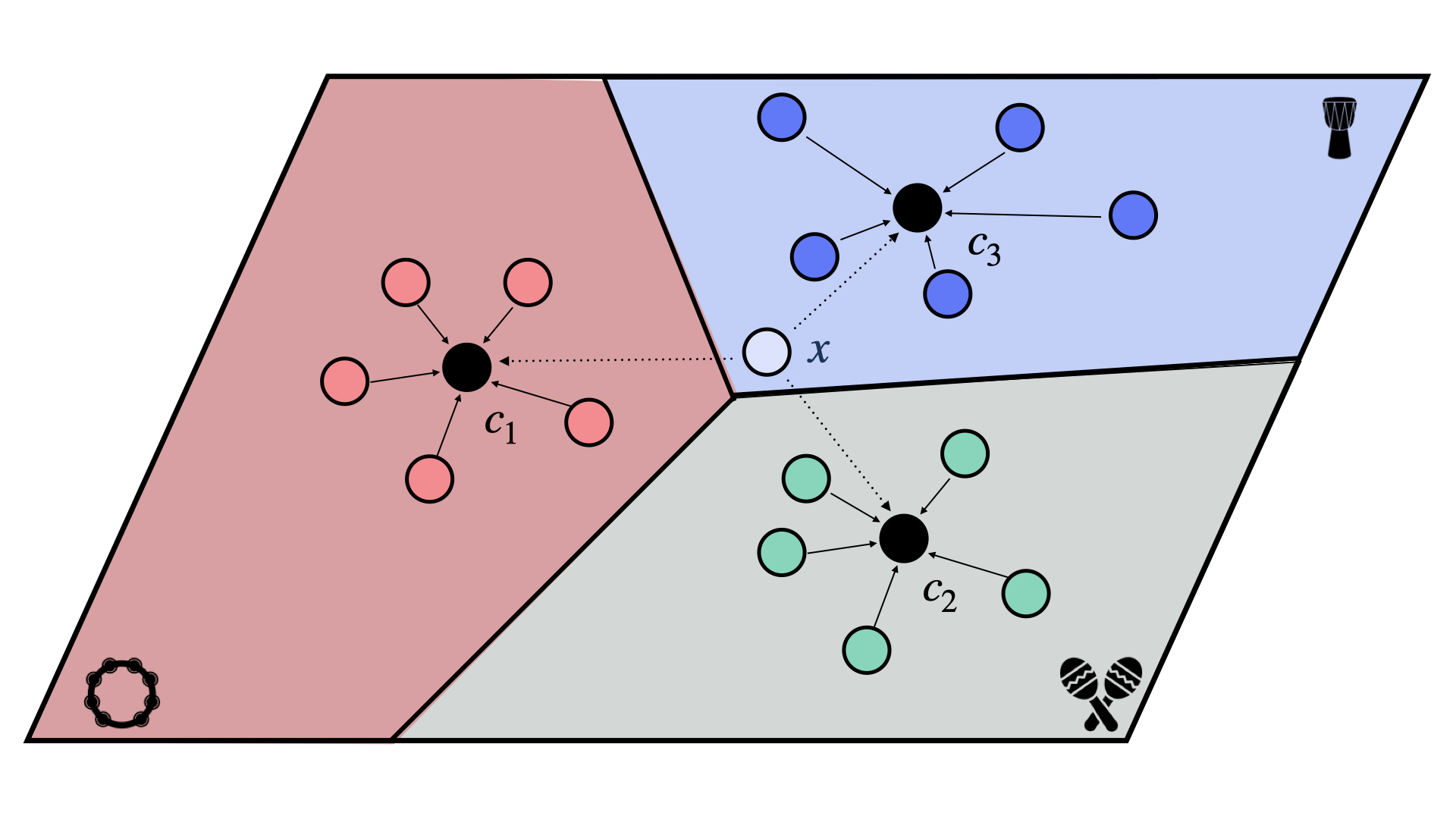
Fig. 9 A prototypical network.#
Requirements (hidden)
%%capture
!pip install torch
!pip install --no-cache-dir --upgrade music-fsl
Creating a Backbone Model#
The first step in making our prototypical network is making a backbone model that can create embeddings from audio examples.
For the sake of simplicity, we’ll be using a fully convolutional model that takes in audio, computes a mel-spectrogram, and then applies a series of convolutional blocks to the spectrograms until it produces a 512-dimensional embedding. We won’t go into much detail about the architecture, since the architecture is not the focus of this tutorial.
Expand the code cell below to see the implementation of the backbone model.
from torchaudio.transforms import MelSpectrogram
from torch import nn
import torch
class ConvBlock(nn.Module):
"""
A convolutional block, consisting of a convolution, group normalization,
ReLU activation, and max pooling.
"""
def __init__(self,
in_channels, out_channels,
kernel_size, stride, padding,
num_groups, max_pool_size
):
super().__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
self.gn = nn.GroupNorm(num_groups, out_channels)
self.relu = nn.ReLU()
self.maxpool = nn.MaxPool2d(max_pool_size)
def forward(self, x):
x = self.conv(x)
x = self.gn(x)
x = self.relu(x)
x = self.maxpool(x)
return x
class Backbone(nn.Module):
"""
A fully convolutional model that produces 512-dimensional embeddings from audio samples.
Args:
sample_rate (int): The sample rate of the input audio.
"""
def __init__(self, sample_rate: int):
super().__init__()
self.melspec = MelSpectrogram(
n_mels=64, sample_rate=sample_rate
)
self.conv1 = ConvBlock(1, 32, 3, 1, 'same', 8, 2)
self.conv2 = ConvBlock(32, 64, 3, 1, 'same',16, 2)
self.conv3 = ConvBlock(64, 128, 3, 1, 'same', 32, 2)
self.conv4 = ConvBlock(128, 256, 3, 1, 'same', 64, 2)
self.conv5 = ConvBlock(256, 512, 1, 1, 'same', 128, 4)
def forward(self, x: torch.Tensor):
assert x.ndim == 3, "Expected a batch of audio samples shape (batch, channels, samples)"
assert x.shape[1] == 1, "Expected a mono audio signal"
x = self.melspec(x)
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.conv5(x)
# pool over the time dimension
# squeeze the (t, f) dimensions
x = x.mean(dim=-1)
x = x.squeeze(-1).squeeze(-1) # (batch, 512)
return x
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
sample_rate = 16000
backbone = Backbone(sample_rate)
print(backbone)
Backbone(
(melspec): MelSpectrogram(
(spectrogram): Spectrogram()
(mel_scale): MelScale()
)
(conv1): ConvBlock(
(conv): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=same)
(gn): GroupNorm(8, 32, eps=1e-05, affine=True)
(relu): ReLU()
(maxpool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv2): ConvBlock(
(conv): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=same)
(gn): GroupNorm(16, 64, eps=1e-05, affine=True)
(relu): ReLU()
(maxpool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv3): ConvBlock(
(conv): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=same)
(gn): GroupNorm(32, 128, eps=1e-05, affine=True)
(relu): ReLU()
(maxpool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv4): ConvBlock(
(conv): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=same)
(gn): GroupNorm(64, 256, eps=1e-05, affine=True)
(relu): ReLU()
(maxpool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv5): ConvBlock(
(conv): Conv2d(256, 512, kernel_size=(1, 1), stride=(1, 1), padding=same)
(gn): GroupNorm(128, 512, eps=1e-05, affine=True)
(relu): ReLU()
(maxpool): MaxPool2d(kernel_size=4, stride=4, padding=0, dilation=1, ceil_mode=False)
)
)
Making a Prototypical Network#
Now for the fun part! It’s time to write the prototypical network itself.
Let’s start by defining a new nn.Module. The backbone model is passed in as an argument to the constructor. We’ll be using this backbone model to compute the embeddings of the examples in the support and query sets.
class PrototypicalNet(nn.Module):
def __init__(self, backbone: nn.Module):
super().__init__()
self.backbone = backbone
Now, we need to define the forward function.
The forward function#
The forward function takes in the support and query sets, which are going to be supplied by the EpisodeDataset that we defined in the previous chapter.
The forward function will carry out the following steps:
Compute the embeddings of the examples in the support and query sets using the backbone model.
Compute the prototypes for each class in the support set.
Compute the distances between the query examples and the prototypes.
Return the logits for the query examples (the negated distances).
The support and query sets are going to be dictionaries with the following keys:
support (dict): A dictionary containing the support set.
The support set dict must contain the following keys:
- audio: A tensor of shape (n_support, n_channels, n_samples)
- label: A tensor of shape (n_support) with label indices
- classlist: A tensor of shape (n_classes) containing the list of classes in this episode
query (dict): A dictionary containing the query set.
The query set dict must contain the following keys:
- audio: A tensor of shape (n_query, n_channels, n_samples)
Let’s get started!
def forward(self, support: dict, query: dict):
"""
Forward pass through the protonet.
"""
1. Computing the embeddings#
The first step is to compute the embeddings of the examples in the support and query sets. We’ll do this by passing the audio tensors in the support and query sets to the backbone model. We’ll update the support and query dictionaries in place to include the embeddings.
# compute the embeddings for the support and query sets
support["embeddings"] = self.backbone(support["audio"])
query["embeddings"] = self.backbone(query["audio"])
2. Computing the prototypes#
Computing the prototypes is a little involved, since we first need to group the support embeddings by class.
We’ll iterate through the indices in the classlist, and grab the subset of embeddings whose target belongs to the current index in the classlist.
# group the support embeddings by class
support_embeddings = []
for idx in range(len(support["classlist"])):
# only keep the subset of embeddings whose target is the current index in the classlist
embeddings = support["embeddings"][support["target"] == idx]
support_embeddings.append(embeddings)
support_embeddings = torch.stack(support_embeddings)
After grouping them, the support_embeddings tensor will have shape (n_classes, n_support, embedding_dim).
Now, we can compute the prototypes by taking the mean of the embeddings for each class. We’ll append the prototypes to the support dictionary in place.
# compute the prototypes for each class
prototypes = support_embeddings.mean(dim=1)
support["prototypes"] = prototypes
The prototypes tensor will have shape (n_classes, embedding_dim).
3. Computing the distances#
The next step in making our prototypical network is computing the distances between the query examples and the prototypes.
Luckily, torch has a very nifty function for computing the pairwise distances between two tensors of shape (batch, n, d) and (batch, m, d), which is torch.cdist.
Because we’re leaving out the batch dimension in this example, we’ll unsqueeze a batch dimension to the query embeddings and prototypes tensors.
Remember that prototypical networks use the squared Euclidean distance, so we’ll set the p norm to 2 and square the result.
# compute the distances between each query and prototype
distances = torch.cdist(
query["embeddings"].unsqueeze(0),
prototypes.unsqueeze(0),
p=2
).squeeze(0)
# square the distances to get the sq euclidean distance
distances = distances ** 2
4. Computing the logits#
Finally, we need to negate the distances so that they can be used as logits (log-probabilities).
# negate the distances to get the logits
logits = -distances
return logits
Expand the code cell below to see the full implementation of the prototypical network.
class PrototypicalNet(nn.Module):
def __init__(self, backbone: nn.Module):
super().__init__()
self.backbone = backbone
def forward(self, support: dict, query: dict):
"""
Forward pass through the protonet.
Args:
support (dict): A dictionary containing the support set.
The support set dict must contain the following keys:
- audio: A tensor of shape (n_support, n_channels, n_samples)
- label: A tensor of shape (n_support) with label indices
- classlist: A tensor of shape (n_classes) containing the list of classes in this episode
query (dict): A dictionary containing the query set.
The query set dict must contain the following keys:
- audio: A tensor of shape (n_query, n_channels, n_samples)
Returns:
logits (torch.Tensor): A tensor of shape (n_query, n_classes) containing the logits
After the forward pass, the support dict is updated with the following keys:
- embeddings: A tensor of shape (n_support, n_features) containing the embeddings
- prototypes: A tensor of shape (n_classes, n_features) containing the prototypes
The query dict is updated with
- embeddings: A tensor of shape (n_query, n_features) containing the embeddings
"""
# compute the embeddings for the support and query sets
support["embeddings"] = self.backbone(support["audio"])
query["embeddings"] = self.backbone(query["audio"])
# group the support embeddings by class
support_embeddings = []
for idx in range(len(support["classlist"])):
embeddings = support["embeddings"][support["target"] == idx]
support_embeddings.append(embeddings)
support_embeddings = torch.stack(support_embeddings)
# compute the prototypes for each class
prototypes = support_embeddings.mean(dim=1)
support["prototypes"] = prototypes
# compute the distances between each query and prototype
distances = torch.cdist(
query["embeddings"].unsqueeze(0),
prototypes.unsqueeze(0),
p=2
).squeeze(0)
# square the distances to get the sq euclidean distance
distances = distances ** 2
logits = -distances
# return the logits
return logits
Putting it all together#
Let’s put all of the pieces we’ve created so far (the class-conditional dataset, the episodic sampler, and the prototypical network) together to get some logits for a training episode.
%%capture
from music_fsl.data import TinySOL, EpisodeDataset
sample_rate = 16000
# create a class-conditional dataset
dataset = TinySOL(sample_rate=sample_rate)
# create an episodic sampler
episodes = EpisodeDataset(
dataset,
n_way=5,
n_support=5,
n_query=20,
n_episodes=100,
)
support, query = episodes[0]
episodes.print_episode(support, query)
Support Set:
Classlist: ['Accordion', 'Violin', 'Oboe', 'Bassoon', 'Alto Saxophone']
Audio Shape: torch.Size([25, 1, 16000])
Target Shape: torch.Size([25])
Query Set:
Classlist: ['Accordion', 'Violin', 'Oboe', 'Bassoon', 'Alto Saxophone']
Audio Shape: torch.Size([100, 1, 16000])
Target Shape: torch.Size([100])
# create our backbone model
backbone = Backbone(sample_rate)
# create a prototypical net
protonet = PrototypicalNet(backbone)
# compute the logits for the sample episode
logits = protonet(support, query)
print(f"got logits with shape {logits.shape}")
got logits with shape torch.Size([100, 5])